Regressions: An Electoral College Example
The most recent presidential election — where Donald Trump beat Hillary Clinton in terms of electoral college votes but lost the popular vote — had many people wondering just how electoral votes were assigned to states.
Suppose you read on the internet that the number of electoral votes a state received, was based on its population. In other words: electoral votes (Y) were determined by population (X).
You go on Twitter or Facebook, and post this “fact”. Of course, being social media, someone challenges you to prove it. Here’s how you do it.
You can do this with a statistical technique known as a regression. Here’s how:
Step 1. Collect the Data
Electoral votes and population are already measurable, you just have to find the data, and hope it’s reliable. Fortunately, Census.gov has the population data and Archive.gov has the number of electoral votes:
Source: Census.gov (https://www.census.gov/data/tables/2016/demo/popest/nation-total.html) for the population data and Archive.gov (https://www.archives.gov/federal-register/electoral-college/allocation.html) for the electoral votes
Step 2. Run a Statistical Operation
If you chart population versus electoral votes, you get the following figure, which suggests using a regression as the statistical operation. A regression finds the best line or curve that fits the data.
A Chart of Population versus Electoral Votes
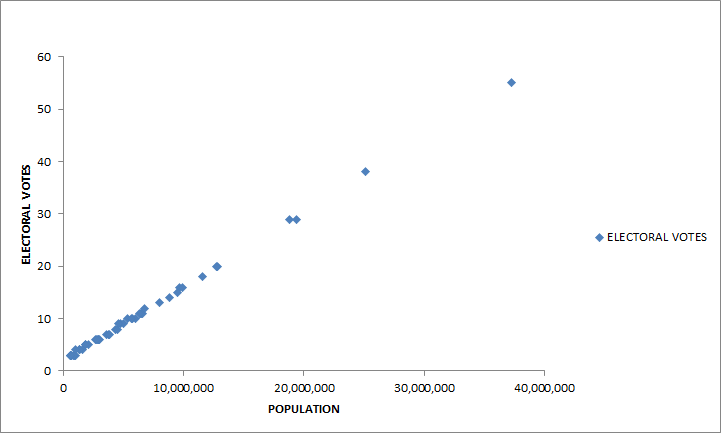
The chart below show the results of the regression. In this case a line best fit the data. This particular regression was done in Microsoft Excel using Data > Data Analysis > Regression, on the table above.
A Regression for Population vs Electoral Votes. Because the curve is a line, this is known as a Linear Regression.
Step 3. See if the Results are Significant
Statistical operations often include a significance measure. For regressions, this measure is R-squared, which ranges from 0 (not significant) to 1 (significant). In the chart above R-squared is .9991 and since it is close to 1 it is significant.
Step 4. Declare your Hypothesis is a Theory, if Significant
Since R-squared is .9991, and this is a significant value, you can proudly post on social media that you’ve proven your theory:
“population determines number of electoral votes.”
And no one can argue with you, because your theories are backed up with reliable data and appropriate statistics.
An Aside on Predictive Power
What’s even better for you is that your theory is predictive. Let me explain.
When you run a regression, you also get the values you need to reconstruct the equation for the curve. For a line, this is an equation of the form:
y=mx+b
If you remember your high school algebra, m is the slope and b is the y-intercept.
You can partly see this equation in the chart above: y=1E-06x+1.9602. I say partly because 1E-06 is really 1.41874E-06. The Excel regression gives the exact values in a table:

Plugging these values in, you get the equation:
ELECTORAL VOTES = 1.41871/1,000,000 * POPULATION+ 1.96
In plain English, take a state’s population, divide by 1 million, multiply by 1.42, add 1.96, and round up.
CHECK
California’s Population: 37,253,956
Divide by 1,000,000 = 37.253956
Multiply by 1.42=52.90
Add 1.96=54.86
Round up: 55 ← CORRECTWyoming’s Population: 563,626
Divide by 1,000,000: .563626
Multiply by 1.42=0.80
Add 1.96=2.76
Round up: 3 ← CORRECT
So the regression yields an equation with the correct value, but what does this equation actually mean? According to Archive.gov:
Electoral votes are allocated among the states based on the Census. Every state is allocated a number of votes equal to the number of senators and representatives in its U.S. Congressional delegation — two votes for its senators in the U.S. Senate plus a number of votes equal to the number of its members in the U. S. House of Representatives.
The 1.42 times the population in millions denotes the number of representatives a state has. The 1.92 denotes the 2 senators. It’s quite astonishing that a simple statistical operation was able to discover precisely what that statement means!